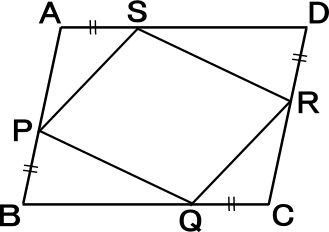
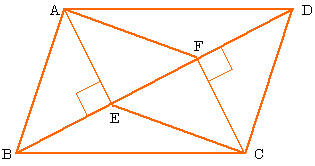
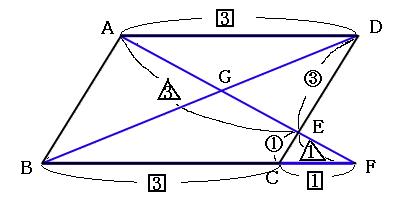
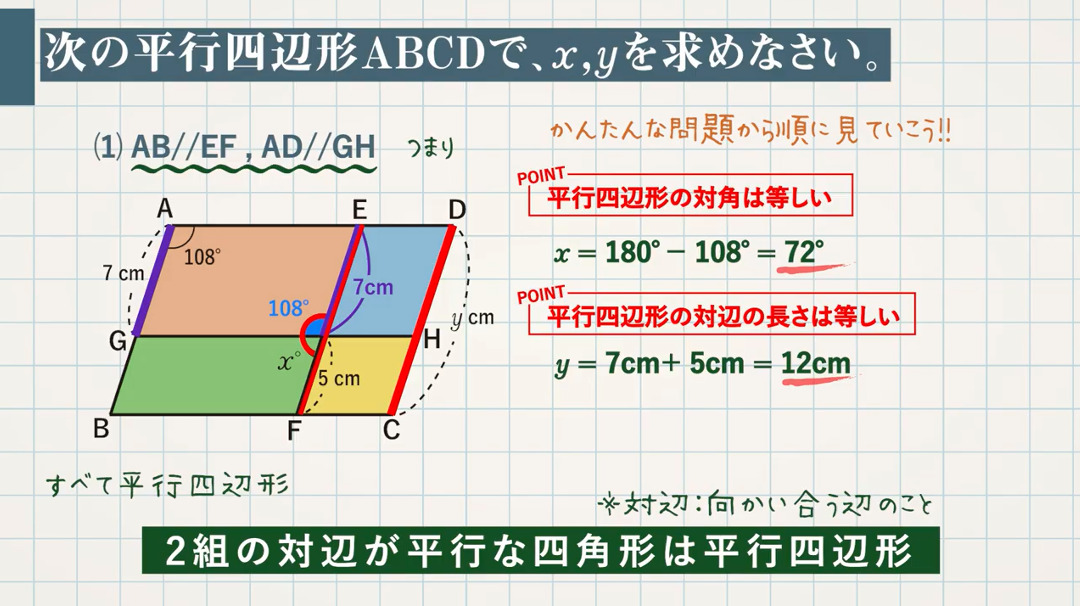
全国学力・学習状況調査 A問題 ① 1 下の四角形ABCDにおいて,「AB//DC,AB=DC」が成り立っています。このことは平行四辺形 になるための条件に当てはまっているので,四角形は平行四辺形になることが分かります。h19Ao=co (平行四辺形の対角線はそれぞれの中点で交わる) ∠aoe=∠cof (対頂角) ∠eao=∠fco (ab//cd 錯角) 1組の辺とその両端の角がそれぞれ等しいので aeo≡ cfo 合同な三角形の対応する辺は等しいので ae=cf ∠def=∠bef(折り返した角) ∠def=∠efb(平行線の錯角)「平行四辺形,長方形,ひし形,正方形の違い」について詳しく知りたい方はこちら 3 平行四辺形の性質を利用する問題 問題1 図の平行四辺形ABCDで,x,yの値を求めなさい。 問題の見方 平行四辺形という条件をもとに,辺の長さや角度を求める問題です。

平行四辺形の証明問題 無料で使える中学学習プリント
平行 四辺 形 問題
平行 四辺 形 問題-問題解説! 問題 下の図の平行四辺形ABCDで、BC上にBE:EC=3:2となる点Eをとり、AEとBDの交点をPとする。 PBEの面積が18㎠のとき、平行四辺形の面積を求めなさい。 平行四辺形の面積を求めたいのですが 全体を一度に求めようとすると難しいので 平行四辺形の半分に当たる ABDの面積を求めてやります。 その後、 ABDの面積を2倍してやれば平行四辺形が求められます角, 円, 外接円, 合同, 作図, 幾何, 中線, 平行四辺形, ひし形, 回転, 正方形, 三角形 中学生でも解ける、大学生でも解けない難問。 ジオジェブラの作図機能を使って考えてみよう。 ジオジェブラは正確なので、図に頼らないで、なぜそのことが言えるのかを




E Ad F A E 4 D Descubre Como Resolverlo En Qanda
平行四辺形の性質と長さや角度を求める問題です。 平行四辺形の性質は小学校で習ったものと同じですが、証明で使えるように定義、性質、条件などを自分で説明できるようにしっかり理解するようにしてください。 基本事項 平行四辺形の定義平行線と角(1) 問題一括 (6,080Kb) 解答一括 (6,744Kb) 平行線と角(2) 平行線と角(3) 三角形の内角と外角(1) 三角形の内角と外角(2) 三角形の内角と外角(3) 角の和を求めてみよう 三角形の内角と外角(4) 多角形の内角 多角形の内角と外角(1) 多角形の内角と外角(2) 合同な図形平行四辺形の性質について問題で確認しましょう。 問 次の平行四辺形について、 にあてはまる数をこたえましょう。 平行四辺形の性質のうち、向かい合う 角の大きさ が等しいことを使います。
中学数学 図形 平行四辺形とは? 定義・条件・性質や面積の公式、証明問題 21年2月19日 この記事では、「平行四辺形」の定義や条件、性質をできるだけわかりやすく解説していきます。 また、平行四辺形の面積の公式や、対角線の角度などの計算問題 「工学系の力学」第2章 問題解答 2-1 ドリル問題 問題1 平行四辺形を作り,合成する。 問題2 f 1 ,f 2 を作用線が交差する点に移動( f 1′,f 2′)。 f 1′, f 2′の合力r′を作図。 r′の作用線を延長して,棒と交わる点を r の 作用点とする。(答#数学問題 #高校入試レベル #良問 #角度「図の平行四辺形abcdにおいて∠acdの大きさを求めてください」シンプルな平行四辺形の角度問題ですが
平行四辺形 例題と練習問題 練習問題 平行四辺形の性質1 平行四辺形の性質2 平行四辺形の性質3 平行四辺形(折り返し) 平行四辺形になるための証明1 平行四辺形になるための証明2 平行四辺形になるため平行四辺形の面積(1) 問題一括 (8,981Kb) 解答一括 (9,158Kb) 平行四辺形の面積(2) 平行四辺形の面積(3) 三角形の面積(1) 三角形の面積(2) 三角形の面積(3) 三角形の面積(4) 台形の面積 ひし形の面積 台形・ひし形の面積 やってみよう 高さと面積の関係 12 百分率とグラフ 割合(1) 問題一括 (8,374Kb)台形,平行四辺形,ひし形 (1)台形と平行四辺形 右の平行四辺形で,辺アイ,アエはそれぞれ何cmでしょう。 また,角ア,ウ,エの角度はそれぞれ何度でしょう。 角ウ (2)ひし形 向かい合った1組の辺が平行な四角形を といいます。
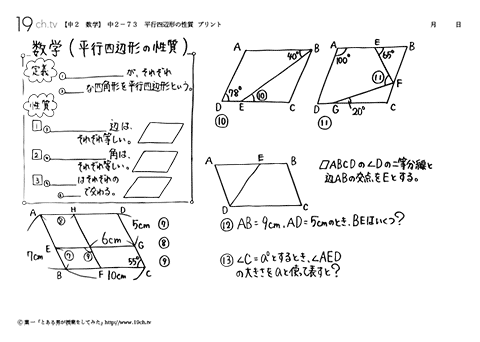



中学2年の数学 動画 平行四辺形の性質の問題 19ch




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ
平行四辺形の向かい合う角は等しいので, a =110° 同様にして,四角形GDFI も平行四辺形で, b =∠DGI=180°- a =180°-110°=70° また,平行四辺形の向かい合う辺は等しいので, x =CF 7 -4 3cm, y AG 10 6 4cm 問題(後期期末)数学が苦手な人でもこの記事を読めば、簡単に平行四辺形に関する証明問題が解ける ようになります。 1平行四辺形とは? 平行四辺形 は、 向かい合う2組の辺が平行な四角形 です。 な問題が,21の都立西にあったのでご紹介します。 問1,問2中2の図形証明分野習った後に解ける 問3相似習った後に解ける 芸術的な難問高校入試 第52回 「平行四辺形の超難しい証明」 出典:令和3年度 都立西高校(独自作成校) 過去問 数学 範囲




中2数学 平行四辺形の証明 練習編 映像授業のtry It トライイット
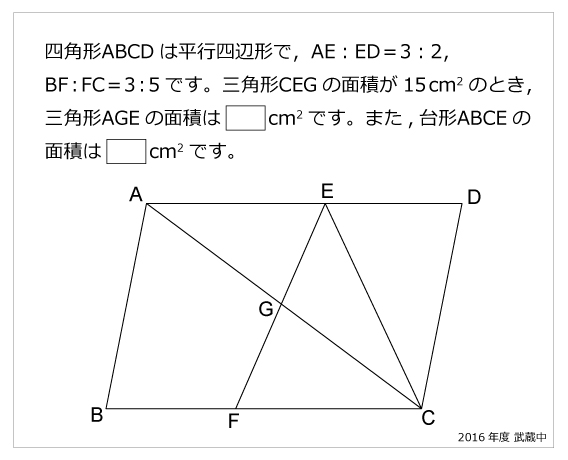



今年の1問 16年武蔵中 平行四辺形 算数星人のweb問題集 中学受験算数の問題に挑戦
上のまとめに示したように「平行四辺形」の定義は「2組の向かい合う辺がそれぞれ平行である四角形」すなわち「 ad//bc , ab//dc 」が成り立つ四角形なので,仮定や結論が「平行四辺形」になっているときは「 ad//bc , ab//dc 」に置き換えるとよい この頁では平行線の性質について,証明の進め方入試問題 数学 愛知県 から,考え方をお伝えしております。ぜひ身につけておこう!受講生の支持トップ級・カリスマ講師年11月1日より第292問 平行四辺形の面積 図形ドリル 5年生 6年生 平行四辺形 相似 相似比 面積比 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。




無料 中2数学 テスト対策 解答プリント 216 図形と合同4 平行四辺形
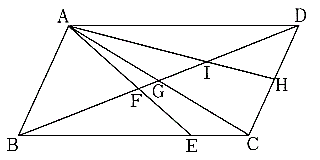



北辰塾 情報局 直撃 中学入試問題 第97回 法政大第二中 相似 平行四辺形の中の三角形
四角形 \(daeb\) が平行四辺形に なるときの、 \(a\) の値を求めなさい。 解説 いろいろ複雑な問題です。 何はともあれ、わかっている情報を図に書き込みます。 情報整理をしないと、スタートがきれません。 で、何をする問題だったか頭を整理しましょう。 平行四辺形の証明の練習問題3 平行四辺形ABCDで, 対角線の交点Oを通る直線を,右の図のようにひき, 2辺AB, CD との交点を, それぞれ, P, Q とします。このとき, OP=OQ となることを証明しなさい。 解答3 △AOP と △COQ で,平行四辺形 \(adbc\) の面積が \(24\) となるとき、 点 \(d\) の座標を求めなさい。 ただし、点 \(C\) の \(y\) 座標は、点 \(A\) の 中学数学の基本から難問までの問題と分かりやすい解説を掲載した完全無料のオンライン学習ページです。



中2数学 学年末テストの証明問題よく出るパターンをまとめてみた 個別指導塾のyou 学舎日記 公式ブログ



平行四辺形を分ける面積比の求め方 算数解法の極意
四角形の4つの辺の中点を結んでできる四角形 はじめに この問題は,GCにとって,とても重要な問題である小学4年生の算数 台形・平行四辺形・ひし形・対角線 問題プリント 小学4年生の算数・台形・平行四辺形・ひし形・対角線の問題を繰り返し練習できるプリントです。平行四辺形2 次の問いに答えよ。 練習問題は印刷してプリントとして使えるものから、pcやスマホから直接できるものまであり、普段の予習復習や定期テスト対策、受験勉強まで中学生の学習を強力にサポートします。




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット
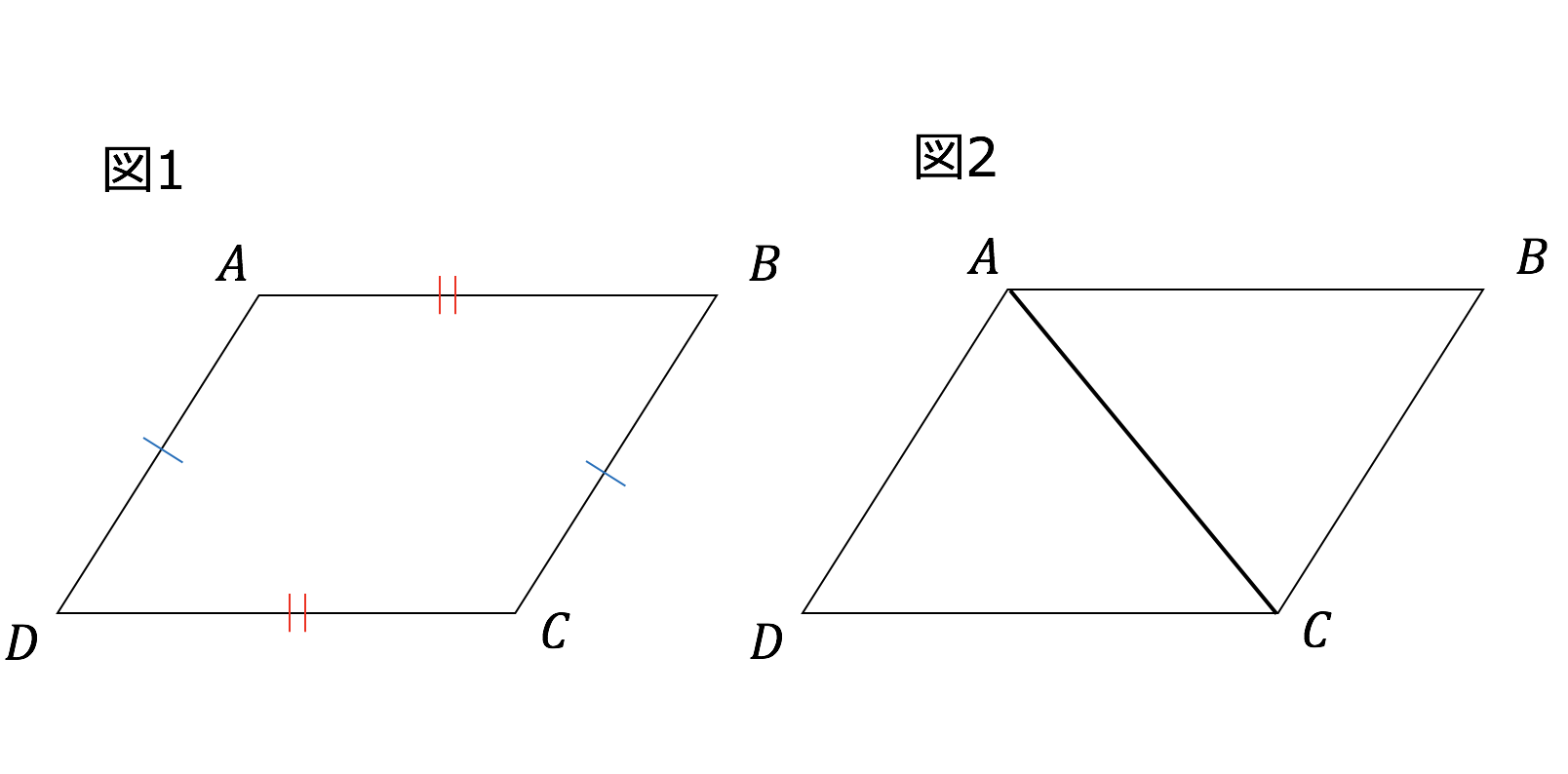



3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ
『 世界一わかりやすい算数問題集シリーズ』の小4算数 「垂直・平行と四角形」です。 例題、練習問題、まとめテストがついています。 これを使って満点目指して頑張ってください!相似比の練習問題(平行四辺形5) 問1図のように、平行四辺形ABCD の辺AD 上にAE:ED =1:2 となる点E をとり、E から 辺AB に平行な直線を引き、辺BC との交点をF とします。第90問 台形と平行四辺形 図形ドリル 6年生 台形 平行四辺形 相似 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げて




平行四辺形の証明問題 無料で使える中学学習プリント




小学生の方が解きやすい 角度問題 ラ サール 数学カフェjr
※例1のような性質は「平行四辺形の2組の向かい合う辺はそれぞれ等しい」と表現されることもある. 問題 四角形 abcd について左欄の性質を証明するとき,どのような仮定からどのような結論を導けばよいか.右の欄から選びなさい. (はじめに左欄の問題を1つ選び続けて右欄の答えを選び 平行四辺形の証明問題 平行四辺形の性質を使った証明の練習問題です。 平行四辺形の性質をしっかり理解してから解くようにしましょう。 また合同な三角形、平行線の錯角、同位角の性質などを利用して証明する問題が多いです。 基本的な証明問題をしっかり練習するようにしましょう。 適期テスト、入試でもよく出題されます。 いろいろなタイプの証明問題数学25章図形の性質と証明「平行四辺形の性質」<応用問題> 組 番 名前 1四角形ABCDが平行四辺形,BE=DFのとき、四角形AECFは平行四辺形であることを証 明しなさい。 F E 2平行四辺形ABCDで,辺AB,BC,CD,DAの中点



第175問の解答




中2数学 平行四辺形であるための条件 例題編 映像授業のtry It トライイット
課題の見られた問題の概要と結果 A 6 平行四辺形の作図 コンパスを使った平行四辺形のかき方について,用いられている平行 四辺形の特徴を選ぶ A 6 正答率 521% 「図形の約束や性質に基づいて作図しこれは中3の実力テストの問題です。答えは分かってます。 ab //dc , ad//bcの平行四辺形abcdがあり、対角線 acをひく。 AB=8cm、ad=10cmのとき、点Cから辺aDまでの距離




中2数学 平行四辺形の性質 練習編 映像授業のtry It トライイット



数b 位置ベクトルの問題を教えてください 平行四辺形abcdの Yahoo 知恵袋



平行性変形でのベクトルの小手技




平行四辺形の面積の求め方 公式と計算例




平行四辺形の面積の求め方 公式と計算例




平行四辺形の定義と性質 証明問題の解き方 数学fun



中学2年数学練習問題 平行四辺形になる条件と証明方法 図形と合同




中2数学 平行四辺形の証明の定期テスト予想問題 Pikuu




平行四辺形の面積を求めるある問題について 身勝手な主張



Hello School 数学 問題集 ハロ数 中2 四角形



中2数学 平行四辺形の証明のポイントと練習問題 Examee
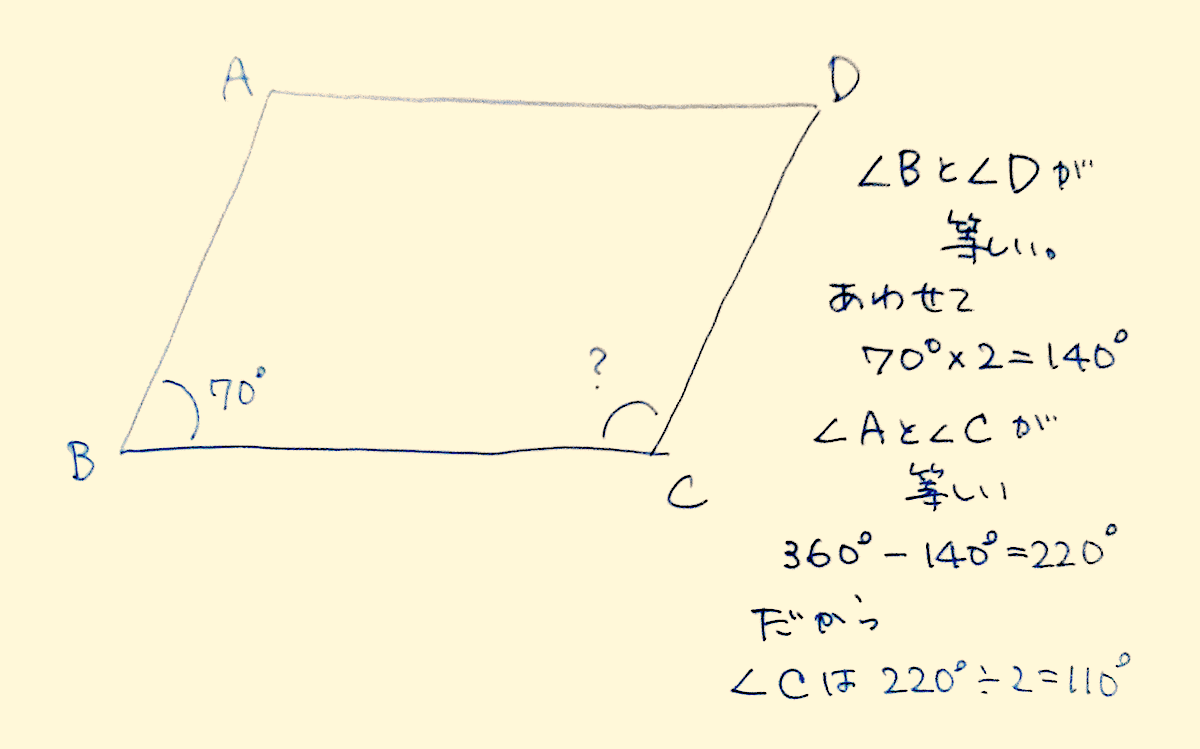



見えることから見えないことへ 平行四辺形の問題で学び方を学ぶ By 岡田 康之 岡田康之のブログ



中2数学 標準問題プリント12 平行四辺形1 性質 問題 230



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




中学数学 平行四辺形になることの証明 その3 中学数学の無料オンライン学習サイトchu Su
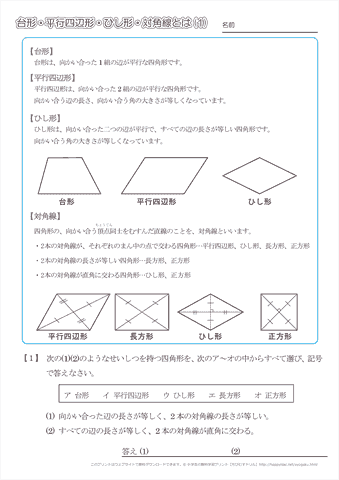



小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生



平行四辺形になるための証明3




四角形 Ict教材eboard イーボード




無料 中2数学 基本解説 解答プリント 230 平行四辺形1 性質



1



平行四辺形 対角線 長さ 計算
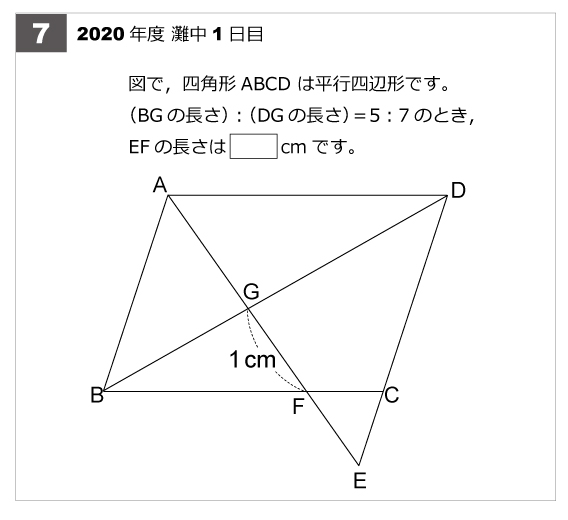



灘中解説速報 年第7問 平行四辺形と相似 算数星人のweb問題集 中学受験算数の問題に挑戦
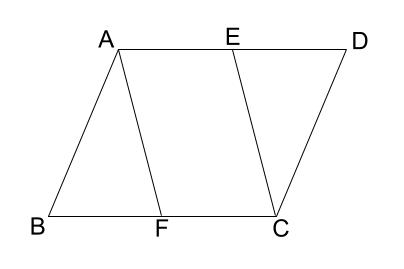



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su




平行四辺形の性質 長さ 角度の問題 無料で使える中学学習プリント




平行四辺形abcdの頂点a Cから対角線bdに垂線を引き 対角線との交点をそれぞれ Clear
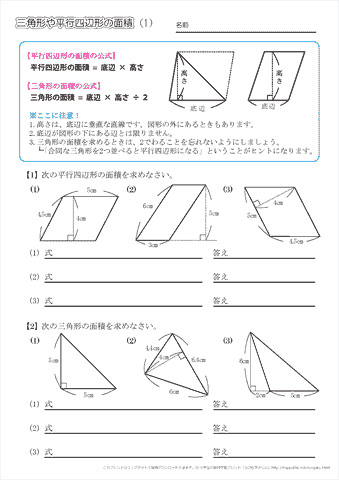



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生




平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学




小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生



1



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




平行四辺形の角度の問題です 基礎的な問題なのですが 教えてください Okwave



平行四辺形の性質の利用2




中2 数学 平行四辺形になるための条件 なんでこうなるのかが わかりません Clear
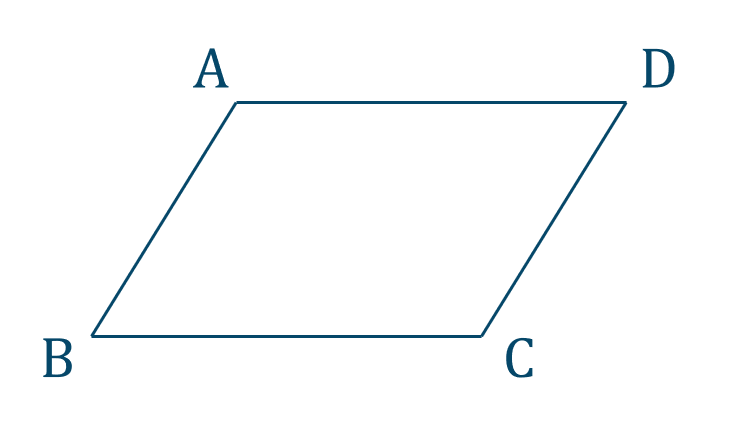



数学b 平行四辺形とベクトルの求め方とコツ ページ 2 教科書より詳しい高校数学



3




中学2年数学 平行四辺形の性質 練習問題5 あんのん塾




無料 中2数学 標準問題 解答プリント 232 平行四辺形3 長方形とひし形




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット
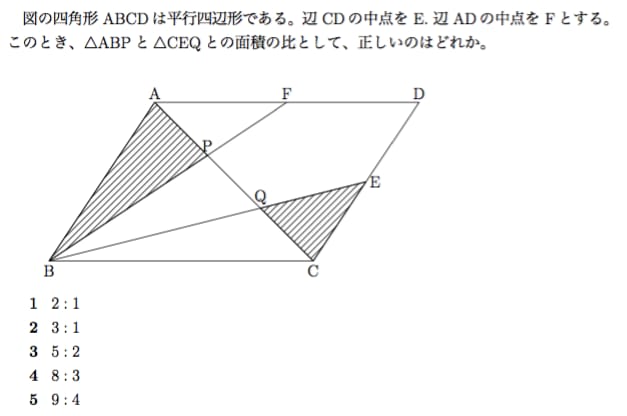



平行四辺形 中点 2つの三角形の面積比 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください



Math 平行四辺形 平行四辺形になることの証明 働きアリ The 2nd
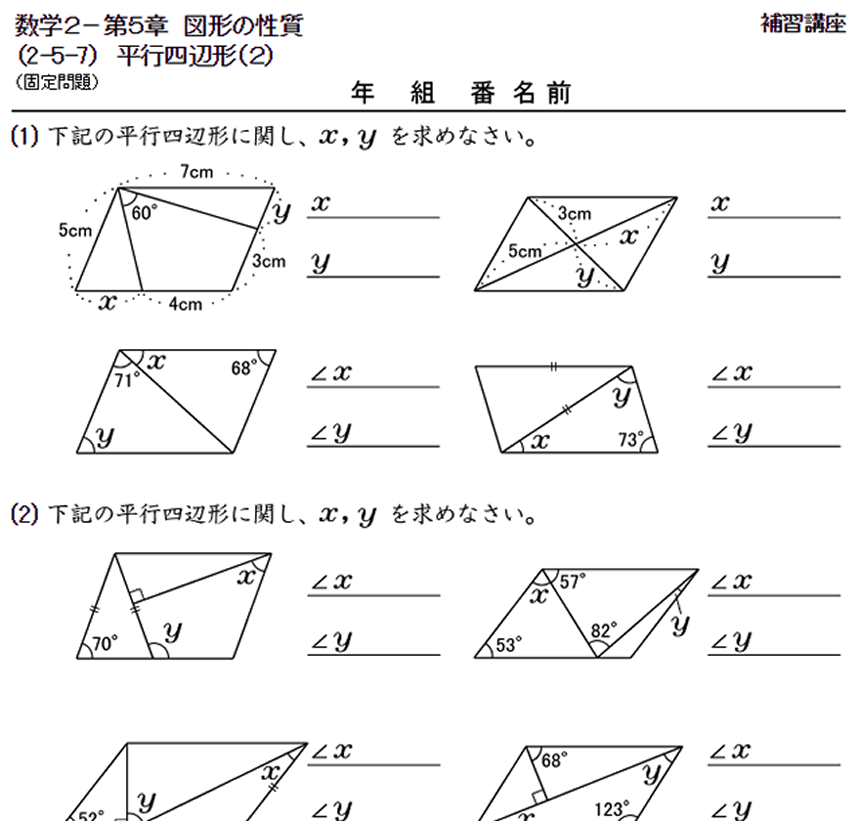



時空先生のドリルプリント 数学の問題
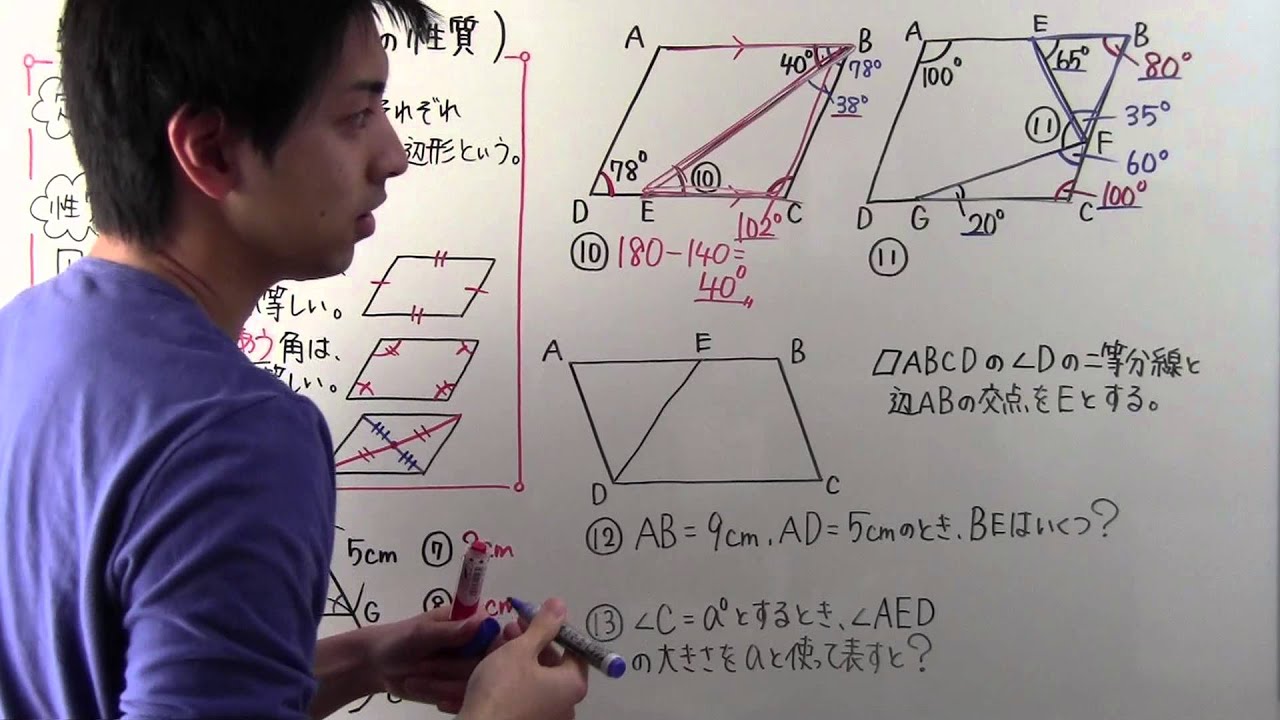



数学 中2 73 平行四辺形の性質 Youtube
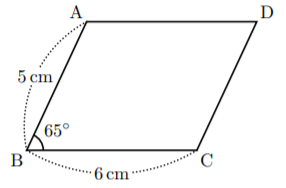



Emath講座 平行四辺形の作図 数樂管理人のブログ
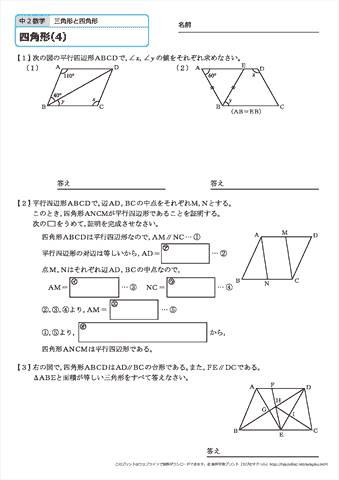



中学2年生 数学 四角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




0 Oa Oc A D Descubre Como Resolverlo En Qanda
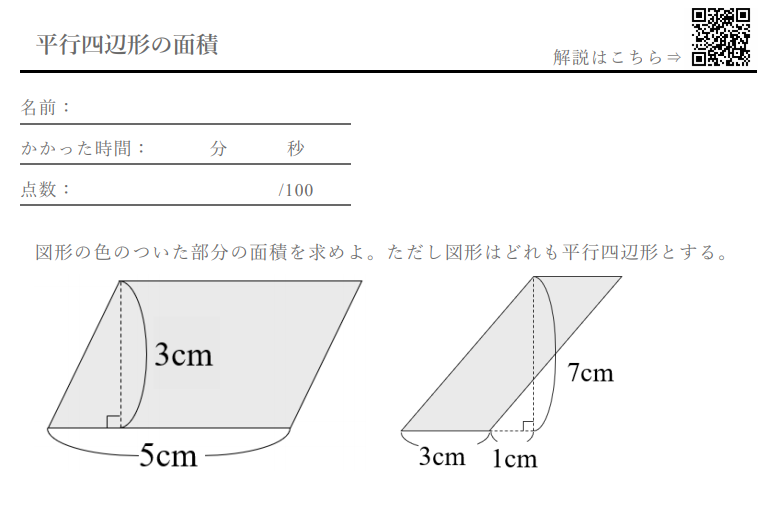



平行四辺形 の面積 計算ドリル 問題集 数学fun



平行四辺形の部分面積は パズル算数クイズ




平行四辺形の性質 と ひし形の性質 を比べる とちぎeライブラリ
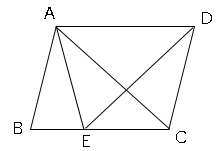



平行四辺形の合同の証明問題と角度を求める問題 数学の要点まとめ 練習問題一覧
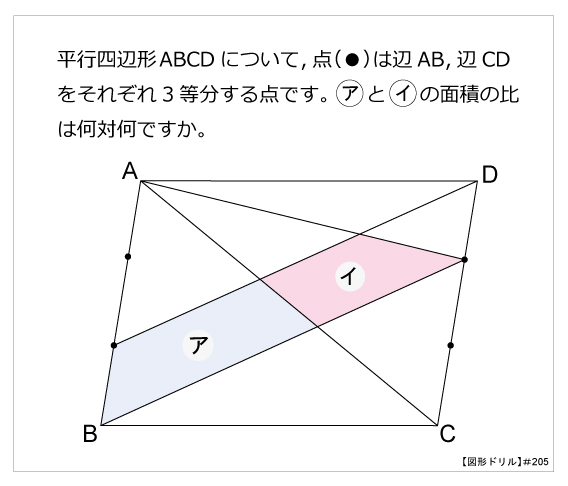



図形ドリル 第5問 平行四辺形内の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦




E Ad F A E 4 D Descubre Como Resolverlo En Qanda
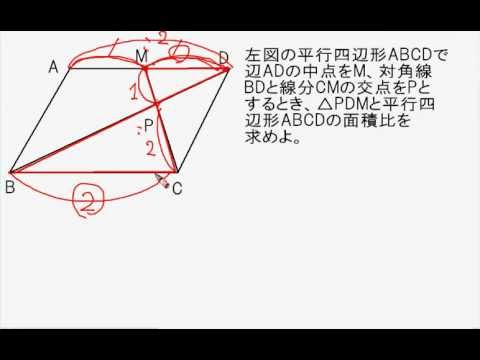



ご質問への解説 平行四辺形面積比 Youtube
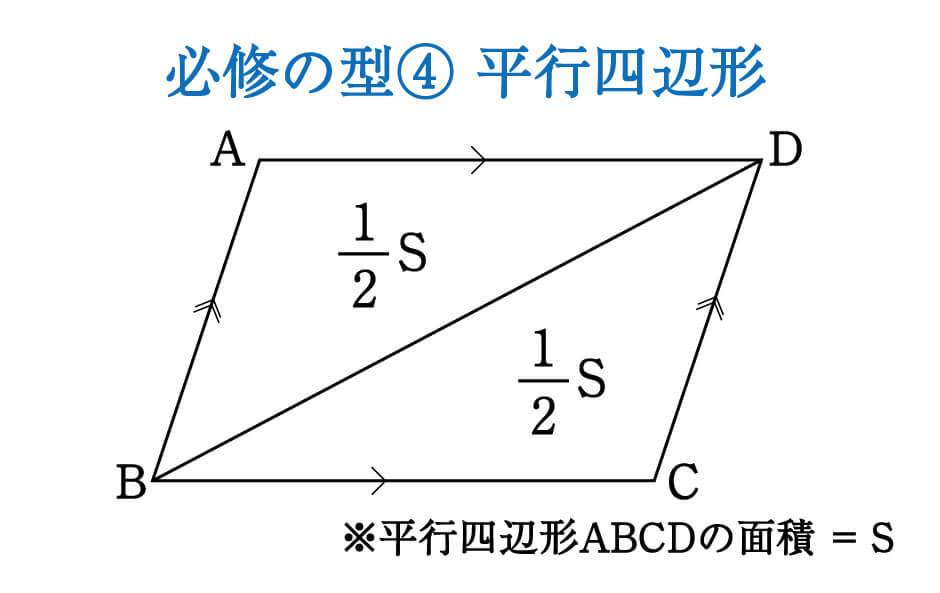



数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
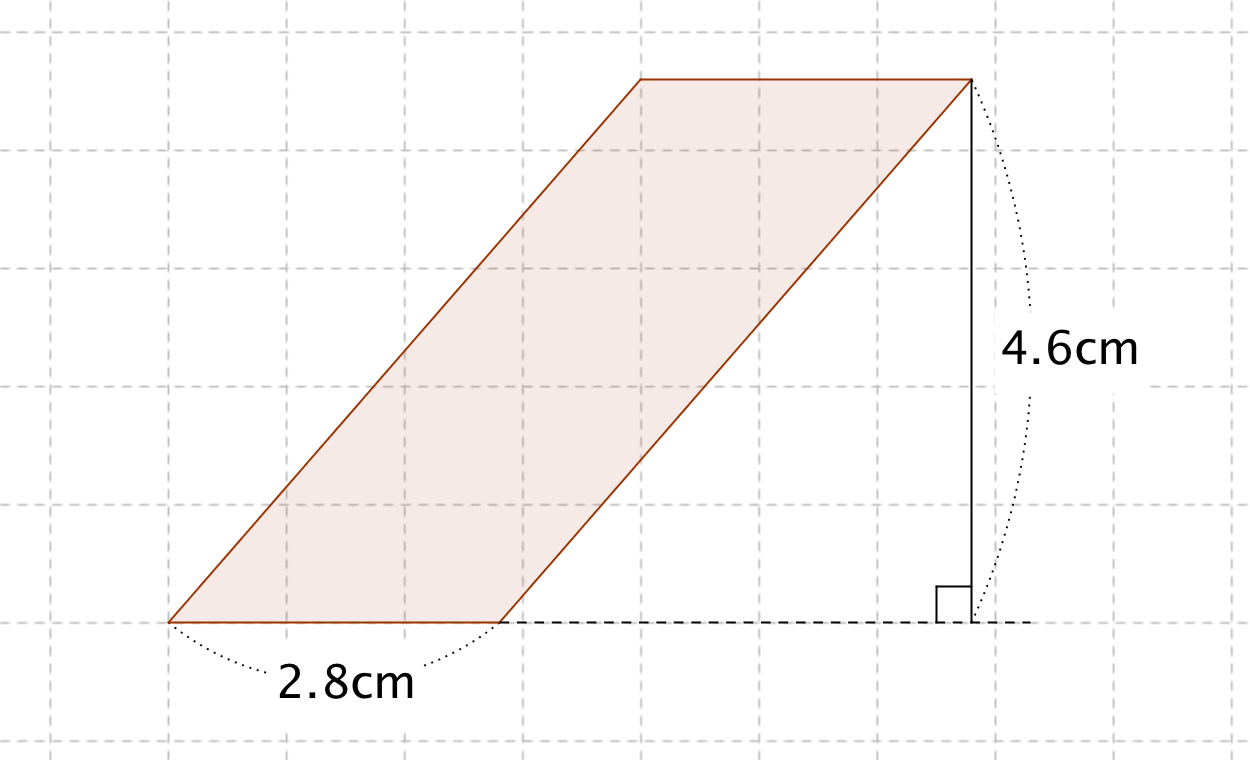



平行四辺形の面積の公式 算数の公式



至急 数学証明平行四辺形の折り目の問題です どなたかご教示お願い致し Yahoo 知恵袋




相似と面積比 よく出る平行四辺形の問題 高校受験対策 公立高校入試 秋田県 Youtube
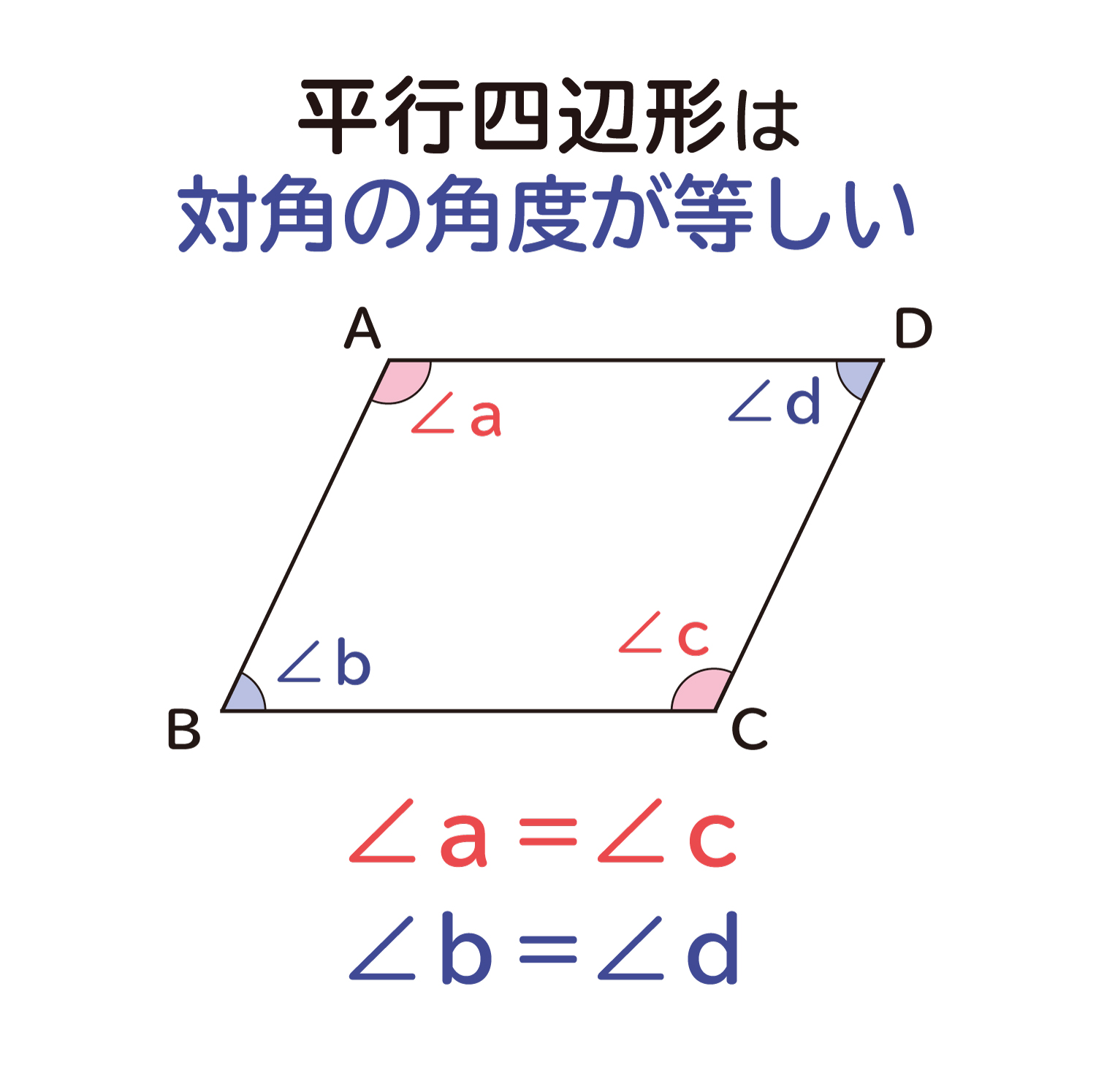



平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル
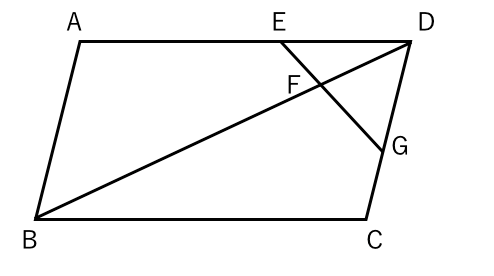



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に




小4算数 Aと同じ角度はどれ 垂直と平行といろいろな四角形 台形 平行四辺形 ひし形 の解き方 教え方 いっしょに勉強しよ



平行四辺形全体の面積の何倍 大阪星光学院中学 2015 これが中学入試に出た図形問題
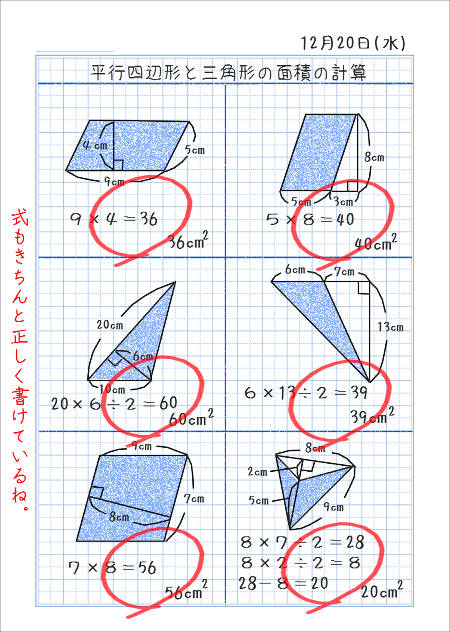



平行四辺形と三角形の面積 家庭学習レシピ
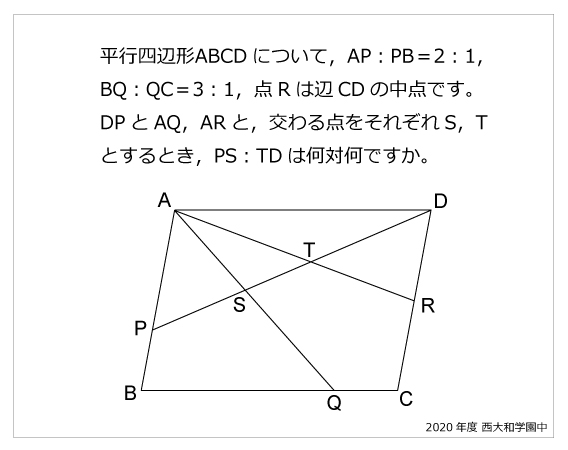



今年の1問 年西大和学園中 平行四辺形と比 算数星人のweb問題集 中学受験算数の問題に挑戦
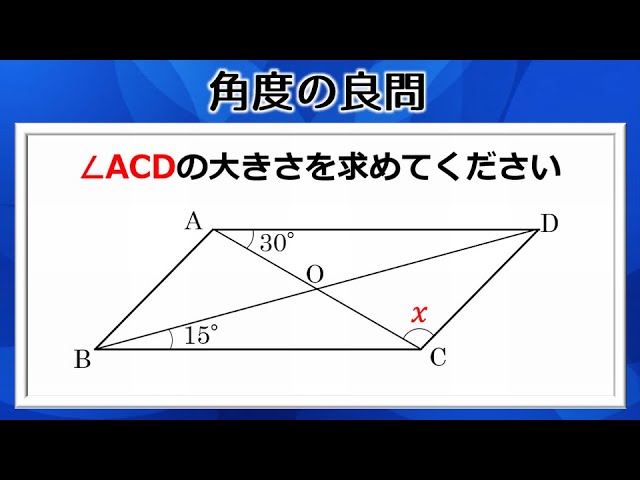



数学角度 高校入試レベルの意外と悩んでしまう平行四辺形の良問 Youtube
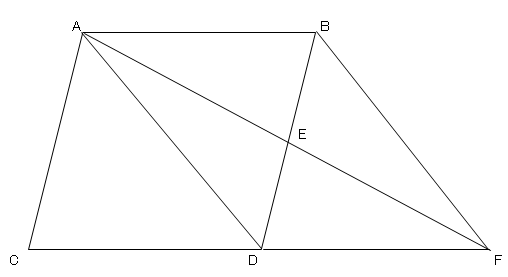



平行四辺形の証明 2 ネット塾
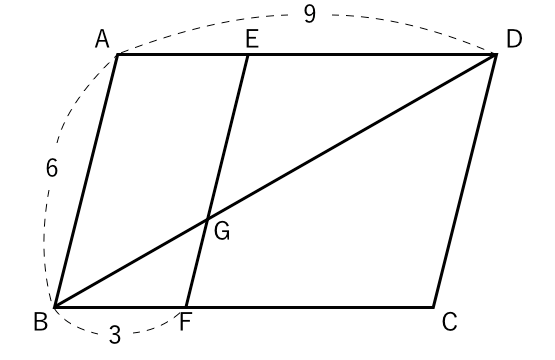



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に
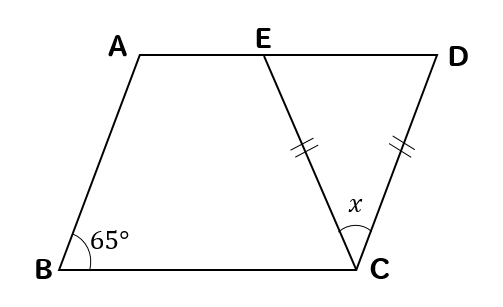



平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ
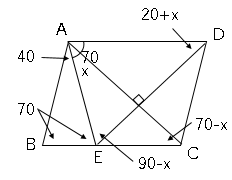



平行四辺形の合同の証明問題と角度を求める問題 数学の要点まとめ 練習問題一覧
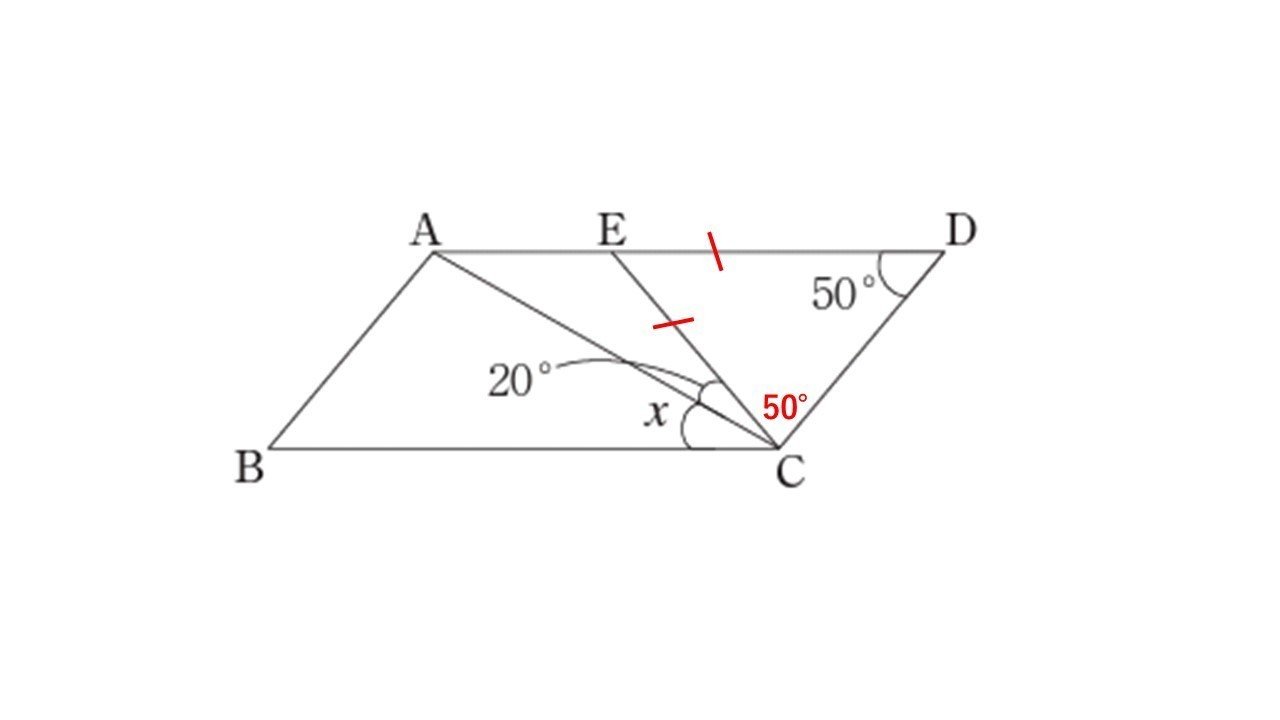



中学数学の平面図形の角度を求める問題を通して学び直しする論理 数学の基礎 タロウ岩井の数学と英語 Note
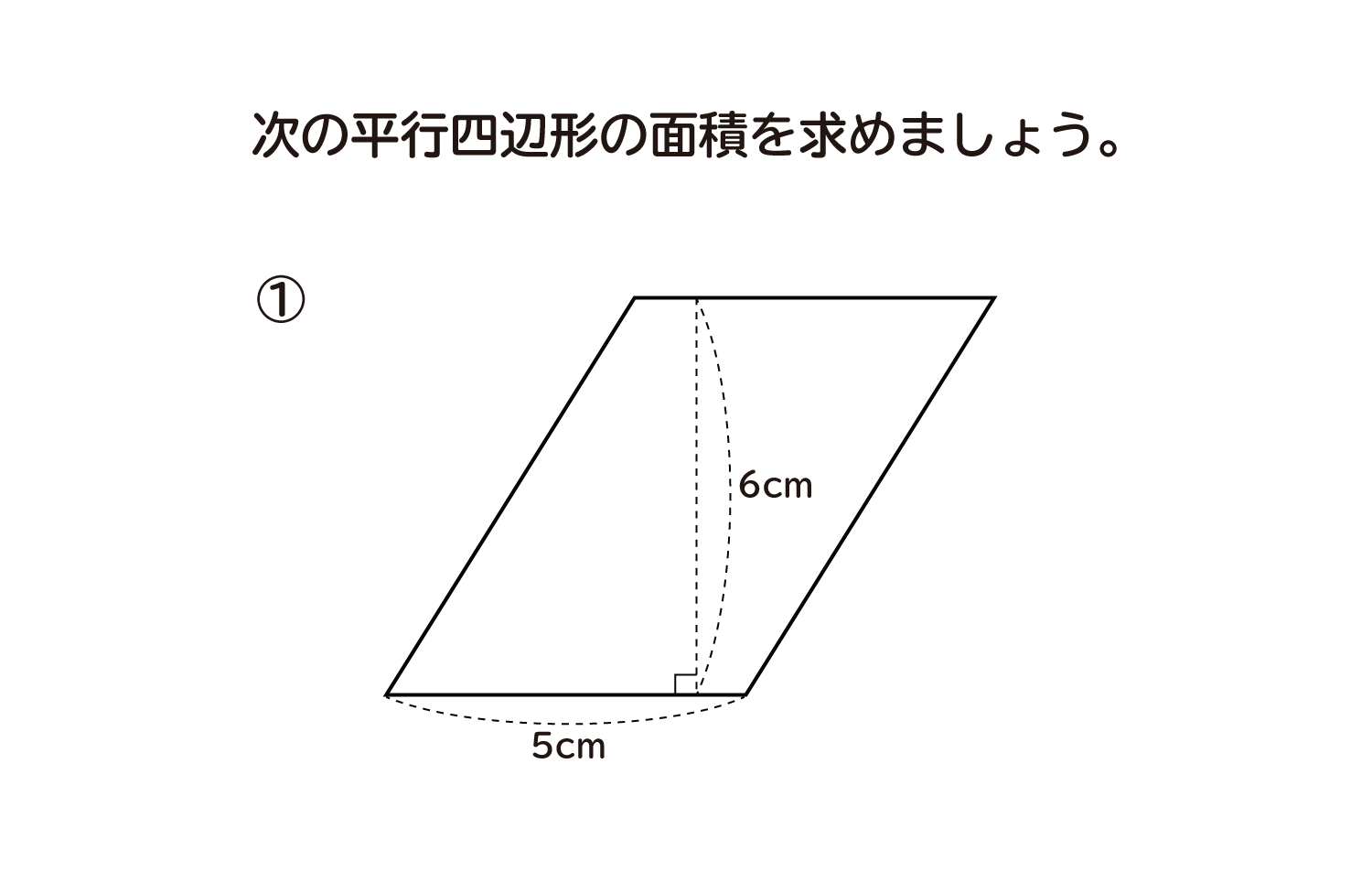



小学5年生 算数 無料問題集 平行四辺形の面積 おかわりドリル
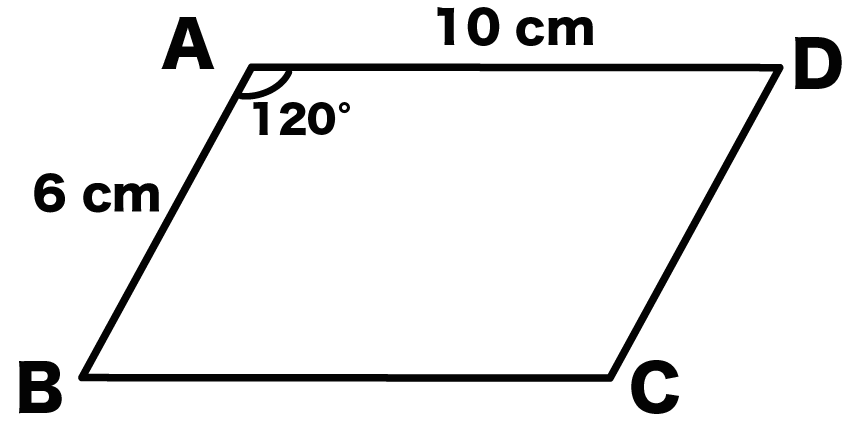



平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



中2数学 基本問題プリント12 平行四辺形1 性質 問題 230
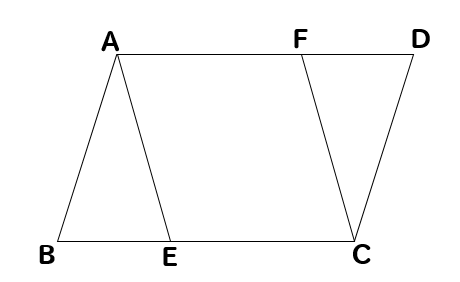



中学数学 平行四辺形の証明問題を徹底解説 数スタ




中点連結定理とは 逆の証明や平行四辺形の問題もわかりやすく解説 遊ぶ数学
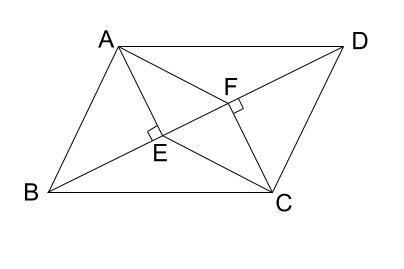



中学数学 平行四辺形になることの証明 その2 中学数学の無料オンライン学習サイトchu Su




Math 平行四辺形 平行四辺形になることの証明 働きアリ
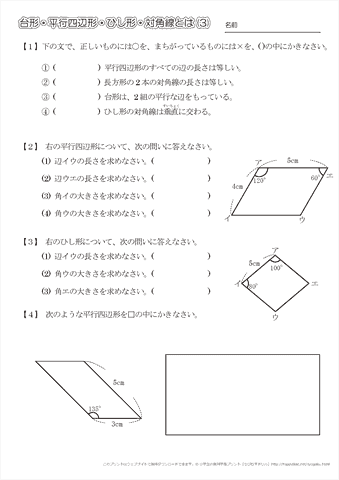



小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生
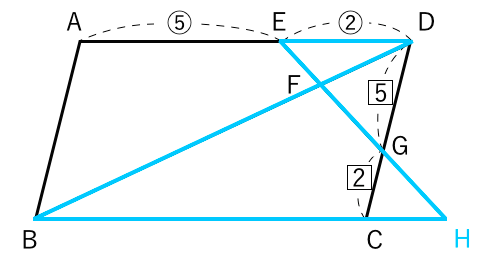



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に



特別な平行四辺形2
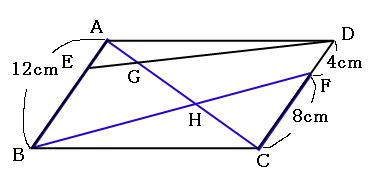



平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ




平行四辺形の問題です 前の続きなのですが 平行四辺形abcdがあ Okwave
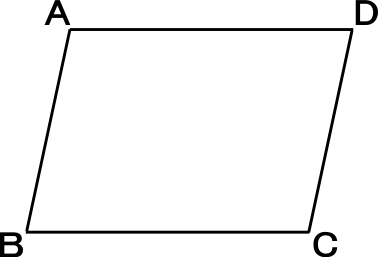



中学2年数学練習問題 図形と合同 平行四辺形の性質と証明問題



角を求める問題




平行四辺形のベクトルの問題です 番の解き方を教えて下さい Clear
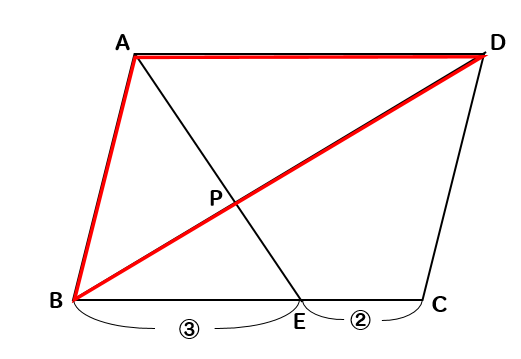



相似 平行四辺形と面積比の問題を徹底解説 数スタ



平行四辺形の垂線 早稲田中学 受験算数問題 07年 どう解く 中学受験算数



1




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



図形問題が驚くほど得意になる基本問題とは あおぞら塾



平行四辺形 二等辺三角形の辺の長さと角 応用問題まとめ 教遊者



Katekyo学院山形 中学生 証明問題 21 1 27



0 件のコメント:
コメントを投稿