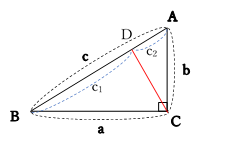
>この定理が何故「ピタゴラスの定理」というのかが分かりません。 N 次元空間 V の中で、 Σn=1~N(,X) と X-Σn=1~N(,X) の組を基底とする 2 次元部分空間を考えてみましょう。 という問題があったのですが,どのように証明すればよいのでしょう
ピタゴラスの定理 問題集- 問題解決のポイント 今回のピタゴラスの定理は、ピタゴラス数を求めるアルゴリズムの問題です。 恐らく競技プログラミングをやられている方などは馴染みがあるのではないでしょうか。 (私は分かりませんでした。。。) ピタゴラス数を全て求める公式として以下の値が用意されていピタゴラスの定理 ピタゴラス(BC5年 BC496年)は、ピタゴラス教という宗教団体と言ってもいいような研究集団のリーダーであったとされている。 したがって、次の定理「三平方の定理」の発見者は、その研究集団のメンバーの一人と思うが
ピタゴラスの定理 問題集のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
 |  | |
「ピタゴラスの定理 問題集」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 | ||
「ピタゴラスの定理 問題集」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「ピタゴラスの定理 問題集」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  | |
「ピタゴラスの定理 問題集」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
「ピタゴラスの定理 問題集」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「ピタゴラスの定理 問題集」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「ピタゴラスの定理 問題集」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「ピタゴラスの定理 問題集」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |
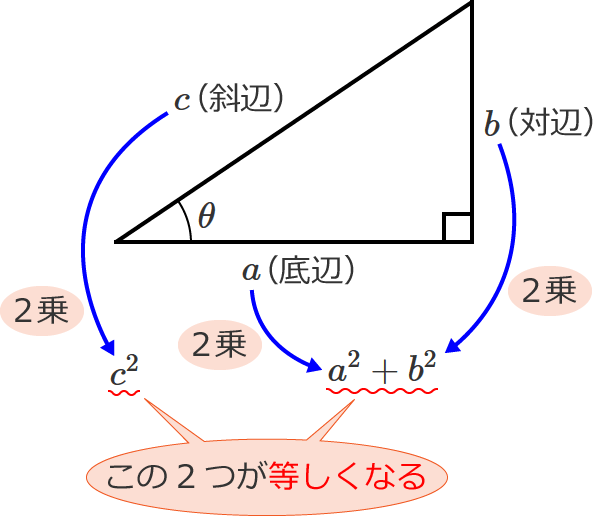
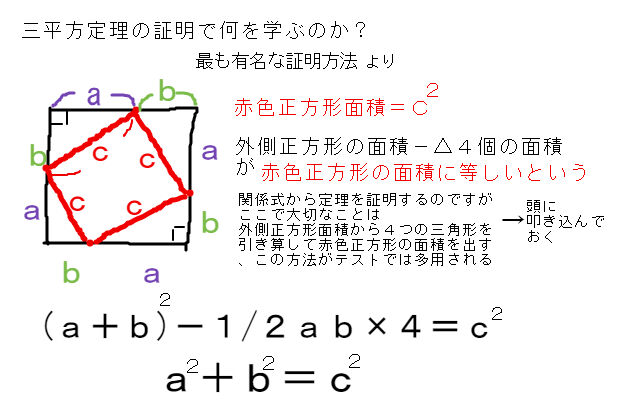
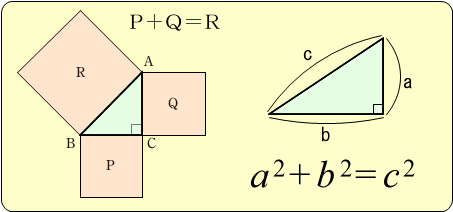
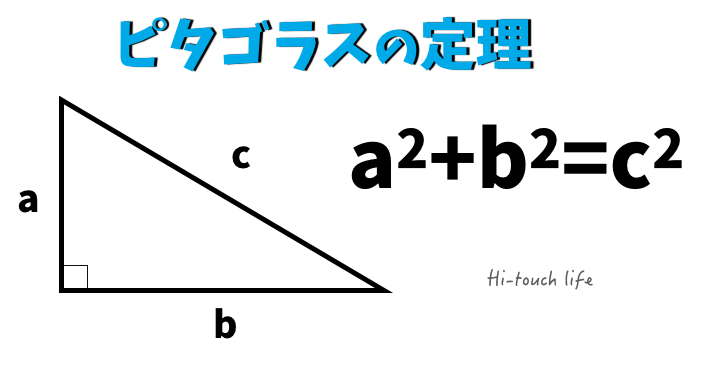
初等幾何学における ピタゴラスの定理 ( ピタゴラスのていり 、 ( 英 Pythagorean theorem )は、直角三角形の3辺の長さの関係を表す。 斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は = が成り立つという等式の形で述べられる 。 三平方の定理 ( さんへいほうのていり ) 、 勾股弦の 本節がこの記事のメインになります.すべての原始ピタゴラス数は,ある 3 3 つの条件を満たす自然数の組 (m,n) ( m, n) によって,完全に表現することができます. 原始ピタゴラス数の公式: (a,b,c) ( a, b, c) を原始ピタゴラス数とする. (つまり, a2 b2 = c2 a 2
Incoming Term: ピタゴラスの定理 問題, ピタゴラスの定理 問題集, ピタゴラスの定理 問題 受験,




0 件のコメント:
コメントを投稿